Module 8. 해찾기 기능 활용 - (2)수학 문제 풀기

해찾기를 이용하여 수학 문제를 푸는 방법에 대해 설명드리려고 합니다.

해석해가 있는 경우이든, 해석해가 없는 경우이든 상관없습니다. 지난 글에서 보여드린 예와 같이 z=exp(x^2)/(x^2+y^2) 함수가 있고, y=1이고, z=10이 되도록 하는 x를 구하고자 한다면, 아래 그림과 같이, x, y, z에 해당하는 셀을 설정하고, z에 해당하는 셀의 함수를 아래와 같이 입력해줍니다. x, y 값이 변경되면 자동을 z값(C2 셀)이 변경될 것입니다.

해찾기를 실행한 후, 목표 셀을 z값에 해당하는 C2로 지정하고, 변경할 셀을 x값에 해당하는 A2 셀로 지정합니다. 값이 음수일수도 있고, 양수일 수도 있기 때문에 '제한되지 않은 변수를 음이 아닌 수로 설정'의 체크를 해제합니다. 변동 범위가 양의 값으로 제한하고 싶다면 그냥 두셔도 됩니다만, 간혹 해찾기가 오류나는 경우에 이 체크 박스를 반드시 확인하셔야 합니다.

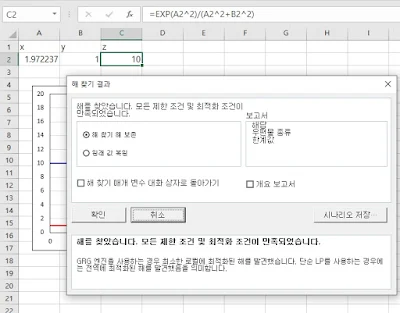
해찾기를 눌러주면, x에 해당하는 A2 셀의 값을 변동시켜 해가 찾아지면, 해찾기 결과를 출력해주고 결과를 유지할 것인지 물어봅니다. z값이 10으로 변했고, x값은 1.972237로 구해집니다.

해찾기의 기본 원리는 변경 셀(x)의 값을 일정량 변동시킨 후, 목표 셀(z) 값의 변화를 확인하여 변경 셀값을 증가시킬지, 감소시킬지를 결장합니다. 이때, x값을 얼마나 변경시킬지 결정해야하는데, 미분값(Δz/Δx)을 사용하게 됩니다. 따라서, 변경 셀의 값을 매우 조금만 변동하더라도 목표셀이 민감하게 반응을 하게 되면, 아무리 많이 반복계산을 하더라도 수렴하지 못하는 경우가 있는데, 해찾기 창의 '해법 선택' 옵션을 눌러 해찾기 방법이나, 최대 반복 횟수, 정밀도 등을 지정해 줄 수 있습니다.

단순 함수값을 구해주는 경우 이외에도 다음과 같이 연립방정식을 풀 수도 있습니다. 예를 들어, y=x^2-5*x+2, y = 3*x+2의 교차점을 구한다고 하겠습니다. 직선과 포물선이 만나는 점이 2개 있으므로, 2개의 해가 있을 것입니다. 그림을 그려보면, 대략 0과 10 사이에 2개의 교차점이 생깁니다. 아래 그림과 같이,

A2=-5, A3=10으로 x의 초기값을 주고, B2=A2^2-5*A2+2, C2=3*A2+2로 입력하고, B2, C2를 복사하여 B3, C2에 붙여넣으면 함수가 복사됩니다. 해를 찾기 위해 목표값을 (y2-y1)의 제곱합을 구할 수 있도록 D2에 '=SUMXMY2(B2:B3,C2:C3)'을 넣어줍니다. D2가 0이 되는 방법은 y1=y2인 경우 밖에 없을 것입니다. 혹은 D2가 최소값이 되도록 해를 찾으라고도 할 수 있습니다.

해찾기에서는 초기값이 매우 중요합니다. 초기값이 설정되지 않으면, x=0에서부터 값을 찾아나가기 시작하는데, x=0일 때, 이미 교차점이 되기 때문에 나머지 x값을 찾지 못합니다. 따라서, 2개의 해를 찾기 위해, 하나의 x는 음수에서 시작하고, 나머지 x를 10에서 시작하도록 초기값을 설정해준 후 해찾기를 실행시킵니다.

이와 같이 해찾기를 실행시킨 결과, 아래와 같이 0과 8이 아닌 근사치로만 계산이 됩니다. 해석적인 방법이 아니라 수치를 대입하는 방법이다보니 계산의 정밀도에 따라, 혹은 지정해둔 반복 계산 횟수에 도달하게 되면 계산을 마쳐버리는 것이지요. 필요하면 해찾기를 다시한번 실행시켜주면 참값에 더욱 근접해가기도 하지만, 정확한 값이 나오지 않을 수도 있습니다. 그러나, 그 오차가 참값과 비교하여 큰 차이가 나지 않으므로, 충분히 유의미한 결과가 되겠지요.

기본적인 해찾기 기능에 대해 설명드렸고, 다음 글에서는 이산 데이터로부터 Fitting하는 방법에 대해 설명드리도록 하겠습니다.