선형 회귀 / Linear fitting의 2가지 기준 - Veritcal Offset과 Perpendicular Offset (1)

<독립변수 X와 종속변수 Y가 모두 동일한 단위를 갖는 측정값일 때 선형 회귀 / Linear fitting하는 방법>

2가지 측정 데이터가 있다고 가정해보겠습니다.

일반적으로 X를 독립변수라고 하고, X값에 따라 변하는 값을 Y라고 합니다. 예를 들어 일정한 속도로 이동하고 있는 물체가 있다고 할 때, 측정시간을 X, 물체의 위치를 Y라고 할 수 있습니다. 이러한 경우, 실험자가 물체의 위치를 X라고 하고, 측정된 시간을 Y라고 하더라도 X-Y 사이에는 선형적인 관계가 있을 것이며, 기울기는 속도 또는 속도의 역수로 나타나게 될 것입니다.

그렇다면, X와 Y를 선택하는 기준이 무엇일까요?

Case I) 서로 인과관계가 있는 두 변수 중 하나는 원인이 되는 변수이고, 나머지는 결과가 되는 경우라면, 원인이 되는 변수를 X, 결과가 되는 변수를 Y라고 표현합니다. 예를 들어, 색소를 물에 혼합했을 때, 색소의 양에 따른 색상을 측정한다고 하면, 색소의 양을 X, 색상을 Y라고 할 수 있습니다.

Case II) 인과 관계가 없는 경우라면, 사용자와 무관하게 측정이 가능한 변수를 X, 측정 오차가 많이 포함될 수 있는 변수를 Y라고 두는 것이 유리합니다. 예를 들어, 시간과 물체의 위치는 서로 인과 관계는 없습니다. 이러한 경우, X, Y는 실험자 마음대로 정할 수 있습니다.

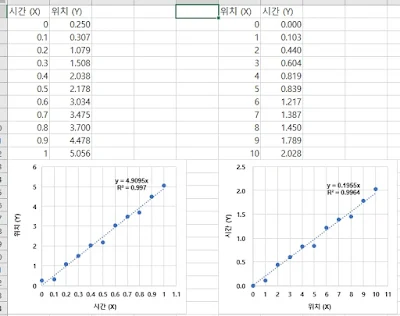
만약, 실험자가 정확히 0.1초마다 위치를 측정할 수 있는 장치(예를 들어, 정확한 시간마다 사진을 찍는 카메라 같은...)를 가지고 있고, 움직이는 물체를 찍는다고 가정해보겠습니다. 시간은 실험자가 아닌 장치가 가진 오차 범위 내에서 비교적 정확하게 동작하는 반면, 물체의 위치는 실험자가 결과로 얻은, 비교적 오차가 발생할 수 있는 데이터입니다. 이러한 경우에는 시간을 X, 물체의 위치를 Y라고 하지요.

이제 다른 방식으로 측정하도록 하겠습니다. 정확하게 1m마다 눈금을 그어두고 물체가 해당 위치를 통과하면 초시계를 이용하여, 통과된 시간을 측정한다고 하겠습니다. 이러한 경우, 위치는 정확하지만, 측정되는 시간은 상당한 오차를 포함할 수 있습니다. 따라서, 위치를 X, 시간을 Y라고 표시하게 되지요.

Case I) 또는 II)의 경우, X-Y간 linear fitting을 위해, 오차를 ∑(Yi-Y)^2이 최소가 되도록 하는 최소 자승법을 이용하면, 쉽게 해결될 수 있습니다. X는 오차가 없으니, Y값에 대한 오차를 최소화하면 그만인 것입니다.

Case III) 만약 두 데이터가 모두 측정된 데이터, 또는 통계치라고 하면 어떻게 해야할까요? 눈금도 대략 1m마다 그어둔 상태에서 수동으로 초시계를 이용해 시간을 측정했다거나, 각각 10명씩으로 구성된 20개의 집단으로부터 평균키와 평균 몸무게를 구한 후, 평균키와 평균 몸무게의 관계식을 구하려고 한다면, X와 Y에 모두 오차를 포함하고 있는 상태가 될 것입니다.

이렇게 되면, Y값만의 오차를 최소화하는 방법으로는 정확한 관계식을 얻을 수 없으며, 다음과 같은 큰 모순에 빠질 수 있습니다.

1) 상관 계수가 0에 근접할수록 기울기도 0에 근접한다 : 아래 그림에서 보시다시피, 데이터의 상관계수가 1 또는 -1에 근접하는 왼쪽 그림에서는 Y값의 오차를 최소화하여 fitting한 녹색선과 X, Y값의 오차를 최소화시켜 fitting한 빨간선이 거의 일치하며, 기울기도 유사한 수준을 보여줍니다. 그러나 오른쪽 그림과 같이, 상관계수가 0에 근접할수록, Y오차를 최소화한 경우보다 X, Y의 오차를 최소화하여 fitting한 결과의 기울기가 2배 이상 크게 나타납니다. 분명 빨간색 타원으로 그려놓은 데이터 분포로 본다면, 빨간색 직선과 같은 fitting 결과가 나와야할 것 같은데 말이지요.

2) X와 Y을 서로 교환한 후, fitting했을 때, 동일한 기울기가 얻어지지 않는다 : 직선의 관계를 가진 데이터라면, X와 Y축을 교환하면, 그 기울기가 교환 전에 구한 기울기의 역수가 되어야 합니다. 만약, 상관계수가 완벽하게 1 또는 -1이 아니라면, X-Y축을 교환한 후, fitting한 결과가 서로 다른 값을 가지게 됩니다. 이러한 현상이 발생하는 이유는, X-Y축을 교환하기 전에는 Y값의 오차만을 최소화한 반면, 축을 교환하고 나서 다시 fitting하게 되면, X값의 오차만을 최소화한 결과이기 때문에 발생하는 문제입니다.

실측된 Y값과 Y 예측치의 차이를 Vertical offset이라고 하고, Vertical offset, 즉 Y값 오차의 제곱합이 최소가 되도록 하는 방법이 일반적인 최소자승법이라고 하며, 대부분의 선형회귀 또는 linear fitting법으로 사용됩니다.

한편, 실측된 (X, Y)값과 예측선의 거리를 Perpendicular offset이라고 하고, 이 거리의 제곱합이 최소가 되도록 예측선을 구하는 방법도 가능합니다. 그러나, perpendicular offset을 최소화하는 방법은 1차식(직선)으로만 fitting이 가능하며, X와 Y가 동일한 단위를 갖는 물리량일 때에만 가능하다는 특징이 있습니다. 만약, 비선형 회귀식/fitting을 구한다거나, 단위가 서로 다른 변수라고 한다면, vertical offset만 사용해야 합니다.

그럼에도 불구하고, X, Y가 동일한 단위를 갖는다면, 선형회귀식/fitting 결과의 대칭성을 가진다는 점만으로도 한번쯤 구현해볼만한 가치는 있을 것입니다.