(xi, yi) 쌍으로 구성된 N개의 데이터가 있다고 할 때, 이 데이터들로부터 오차가 가장 작아지는 함수를 찾아내는 것이 regression 혹은 fitting이라고 합니다. 다만, 통계에서는 regression이라고 하고, 공학에서는 함수 fitting이라고 많이 표현하는데, 결과만 본다면 비슷합니다.
다항식의 경우, 측정된 (x,y)로부터 아래와 같이 행렬 계산만 하면 되기 때문에 오차를 최소화하는 별도의 알고리즘은 필요가 없습니다. 또한 속도의 차이가 있을 뿐, 특수한 경우는 제외하고 다른 결과가 출력되는 것은 아닙니다.
그러나, 다른 형태의 비선형 함수 및 이들의 결합 함수들은 iteration이라고 하는 오차가 최소화되도록 반복 계산을 수행하여 결과를 얻게 됩니다. iteration은 알고리즘에 따라 해를 찾을 수도 있고, 찾지 못할 수도 있습니다. 즉, 알고리즘에 따라, 또한 해결하려는 문제에 따라 결과가 다르게 출력된다는 것이지요. 이러한 비선형 부분에 대한 iteration은 엑셀의 해찾기 기능으로 보완해줄 수 있습니다. 관련된 내용은 향후에 추가해보도록 하겠습니다.
다항식에 대한 fitting의 원리는 아래와 같습니다.
만약 y가 x의 n차 다항식의 관계라고 한다면,
과 같이 표현할 수 있습니다. 측정된 결과가 이러한 관계를 따른다면, 오차는 위의 다항식에 x값을 대입해서 얻은 y값과 측정값으로 얻은 y값의 차이가 최소가 되어야 합니다. 여러 측정값에 대하여 이 차이의 제곱합을 오차라고 한다면, 오차의 합이 최소가 되도록 a_0~a_n 값을 찾아주면 됩니다.
a_0~a_n에 대하여 이 값들이 변할 때, 오차가 최소인 점에서 오차를 각각의 계수로 편미분한 값이 0이 되어야 합니다.

위의 편미분식은 총 n+1개가 존재하게 되고, 미지수가 a_0부터 a_n까지 총 n+1개이므로 선형방정식으로 변하게 됩니다. 결과적으로 아래와 같이 n+1차 행렬식으로 변환시킬 수 있고, 이 값들을 계산한 후, 역행렬을 취해주면, a값들을 모두 구할 수 있습니다.
일반적인 경우에는, 위의 행렬을 풀면 대체로 잘 맞는 결과를 출력해줍니다만, 간혹 문제가 있을 수 있습니다. 이는 컴퓨터에서 계산에 사용되는 유효숫자의 문제 때문에 발생하는 것인데, 위의 행렬식의 문제가 아니라, 데이터 갯수와 데이터 값의 분포 때문에 나타나는 문제입니다. 잘 이해가 안가실 수 있어서 예를 들어 보겠습니다.
예를 들어, x의 변동 범위가 (10^3, 10^3+1) 구간이라고 하겠습니다. x의 평균값에 비해 지나치게 좁은 범위에서 값이 변하게 되면, 위의 행렬에서 ∑x^2n을 계산한 결과는 10^6n 정도의 값을 가집니다. 만약, 3차식으로 계산한다고 하면, 10^6n=10^18 수준의 값을 가지게 되는 반면, ∑x를 계산한 결과는 10^3 정도의 값을 가지게 됩니다. 따라서, 컴퓨터의 유효숫자 범위가 12자리라고 해도 ∑x^2n에 ∑x을 더해봐도 덧셈이 이루어지지 않습니다. 반면, y의 경우, 모든 계산에 y의 1차항에 해당하는 값만 계산에 참여하게 되니, 이러한 문제가 발생하지 않습니다.
위의 계산은 x의 변동폭이 x의 평균값 대비 1/1000인 경우에 대해 계산한 결과인데, 이러한 상황은 매우 자주 있는 일입니다. 따라서, 코딩은 전혀 문제가 없는데, fitting 결과가 전혀 엉뚱하게 되는 경우가 종종 발생됩니다.
이를 해결하기 위해서는 x값을 평균내어 x-<x>로 평행이동시킨 후, 위의 행렬식을 이용하여 y(x-<x>)를 계산하고, 다시 y(x)로 평행이동해 주어야 제대로된 fitting 결과를 얻을 수 있습니다. 어쨋거나 이 모든 계산은 행렬계산에 기반되어있으므로, 순차적으로 함수를 작성해보도록 하겠습니다.
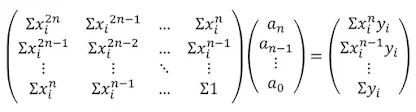


댓글 없음:
댓글 쓰기
의견이나 질문이 있으신 분은 언제든지 댓글을 달아주세요~